Understanding the Concept of Average
Seeking assistance to grasp the concept of average might be beneficial. The essence of averages lies in their ability to measure the central tendency, which is a single value that represents a dataset. However, explaining when to utilize a specific type of average can be challenging. An attempt to clarify this is welcome, yet if there’s a differing viewpoint, receiving correction is appreciated.
Calculating an average involves assessing the central tendency: a unique figure that symbolizes the dataset. However, datasets can vary widely in their distributions, dimensionality, or types (employing computer science terminology). Whether dealing with lognormal distributions, rates, or classes, this diversity necessitates the use of different kinds of averages to accommodate the varying data characteristics.
The Harmonic Mean Equation, a fundamental tool in statistical analysis, is intricately intertwined with the topics discussed in the October Linkfest article. If you found this intriguing, you may also like to delve into related statistical methodologies and their applications.
The Arithmetic Mean: A Basic Yet Sensitive Measure

The arithmetic mean, often regarded as the most straightforward and universally recognized measure of central tendency, has its limitations, particularly in terms of robustness. Statistically, its accuracy can be significantly compromised by outliers—data points that deviate markedly from the expected pattern or model of the data set. These outliers are not just anomalies; they are crucial in various contexts, especially in fields like exploration where the biggest finds in a gas prospect, though rare, are vital. This sensitivity to outliers means that while the arithmetic mean is easy to compute and understand, it may not always provide the most reliable representation of a data set, especially in the presence of significant variability.
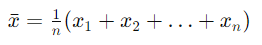
Geometric Mean: A Measure Beyond Arithmetic Averages
Comparable to the arithmetic mean, the geometric mean stands as one of the fundamental Pythagorean means. However, it typically equals or falls below the arithmetic mean in value. Its essence is visually depicted through a simple geometric representation: envision the geometric mean of two values, a and b, as the length of a side of a square equivalent in area to the rectangle formed by a and b. It’s crucial to note that the geometric mean is applicable solely to positive numbers. When does it find utility? Consider scenarios involving quantities following exponential distributions, such as permeability. Moreover, when dealing with data normalized to a reference value, the geometric mean emerges as the sole appropriate measure to employ.
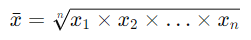
Harmonic Mean: A Lesser-Known Yet Essential Measure
The harmonic mean, often overlooked among the Pythagorean means, invariably equals or falls below the geometric mean. Referred to occasionally, albeit facetiously, as the subcontrary mean, its tendency is towards smaller values within a dataset. However, it’s critical to discern that if these smaller values appear as outliers, it signifies an issue rather than a beneficial trait. The harmonic mean finds its forte in dealing with rates. For instance, when calculating average speed over a distance covered at varying rates, such as driving 10 km at 60 km/hr followed by 10 km at 120 km/hr, the harmonic mean accurately portrays the overall average speed—80 km/hr—contrary to the misleading 90 km/hr that the arithmetic mean might suggest.
| 1,2,2,3,5,9 | 0.01, 0.02, 2, 3, 100,110 | -1.1,-1.1,-0.1,0.1,3,1.2,2.6 | |
| Arithmetic | 3.43 | 35.8 | 0.272 |
| Geometric | 2.71 | 1.54 | Undefined |
| Harmonic | 2.23 | 0.0398 | Undefined |
| Median | 2 | 2.50 | 0.0150 |
| Mode | 2 | Undefined | -1.1 |
| RMS | 4.28 | 60.7 | 1.35 |
Exploring the Concept of Median Averages
- The median serves as the pivotal point within sorted data, embodying the quintessential average: positioned at the midpoint, with 50% of values lying above and 50% below;
- In cases where there’s an even count of data points, it becomes the arithmetic mean of the two central values;
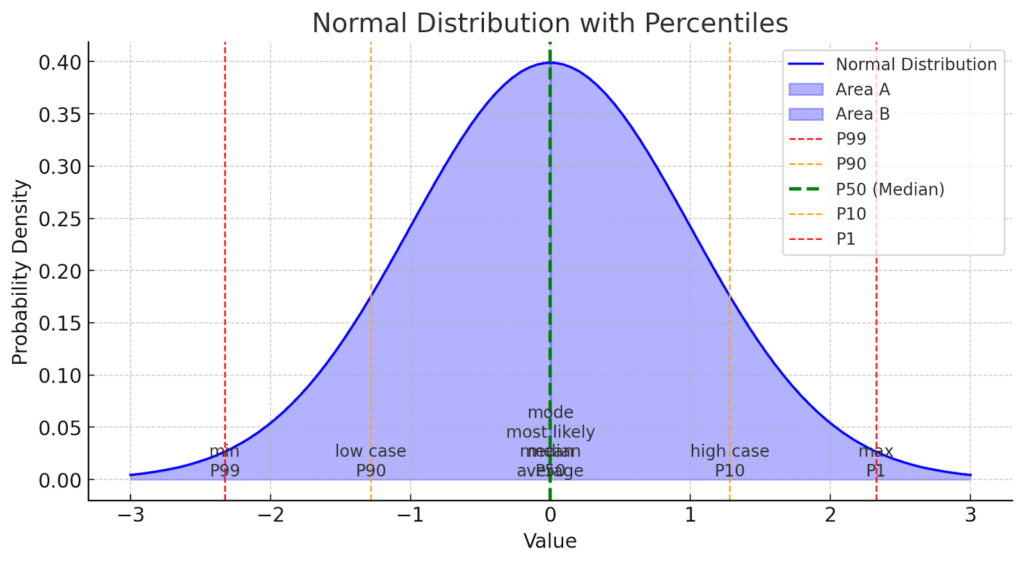
- Within probability distributions, the median often assumes the moniker “P50.”;
- Notably, in positively skewed distributions, such as those prevalent in petroleum geoscience, it surpasses the mode yet remains smaller than the mean.
The Essence of Mode Averages
The mode, often referred to as the “most likely” outcome, represents the most frequently occurring result within a dataset. It finds its primary utility in analyzing nominal data, which includes classes or names, as opposed to the numerical values discussed previously. For instance, while the name “Smith” may not be the statistical ‘average’ name in the US, it can be considered as the central tendency among names due to its frequency. A notable application of the mode lies in simple voting systems, where the candidate with the highest number of votes emerges victorious. When dealing with data categories like facies or waveform classes, the mode emerges as the sole meaningful average.
Exploring Noteworthy Averages
Many geophysicists are familiar with the concept of the root mean square, also known as the quadratic mean, as it provides a measure of magnitude that is independent of sign. This property makes it particularly useful for analyzing sinusoidal variations around zero.
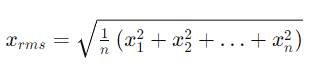
Another average worth acknowledging is the weighted mean. While it may seem intuitive in certain scenarios, such as when averaging datasets with different populations, its application can sometimes be less obvious. For instance, when considering the perception of data points, the need for a weighted sum may not be immediately apparent.
Skewness: Overlooking Swanson’s Mean?
A recent conversation with geo-stats enthusiast @fraserrc brought to light an omission in my earlier mentions – the omission of Swanson’s Mean. This straightforward estimation method is perfect for roughly skewed distributions, often lognormal, using P90, P50, and P10 values, and is particularly user-friendly for those in the petroleum geology field.
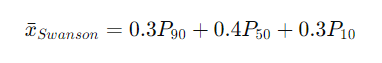
The method owes its development to Roy Swanson, a former geologist at Exxon, and his colleagues from the University of Aberdeen. It gained wider recognition through the educational efforts of Peter Rose, particularly his influential courses and the comprehensive book “Risk Analysis and Management of Petroleum Exploration Ventures.”
Conclusion
Averages are far from a monolithic concept. Depending on datasets’ characteristics and the specific requirement, different averages – Arithmetic, Geometric, Harmonic, Median, Mode, Root Mean Square, and Weighted Mean- can be chosen. What remains constant, however, is the importance of selecting the right ‘average’ to gain accurate insights from your data. Understanding the properties and uses of each average ensures reliable interpretations and robust decision-making.