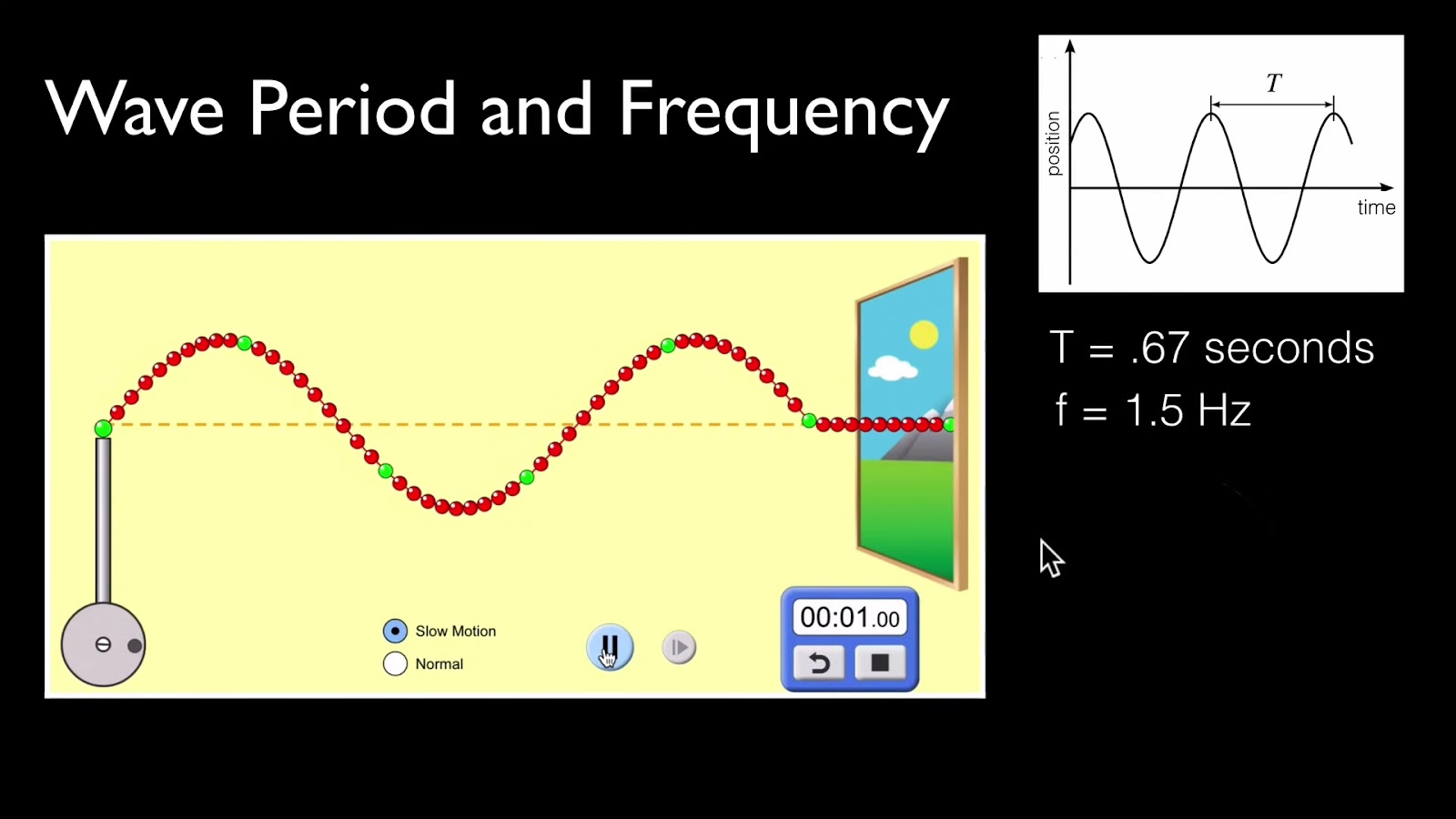
Understanding Wave Period: What It Measures

Waves, an intrinsic component of the natural world, manifest in diverse manifestations, spanning the vast expanses of oceans, the ethereal domain of the atmosphere, and even within the intangible realm of sound. A pivotal attribute employed to elucidate waves is their period, a fundamental metric that unveils profound insights into their behaviors, energetic properties, and dynamic interactions. Throughout this discourse, we shall embark on an exploration of the significance imbued within wave periods, illuminating their essence, the methodologies employed in their quantification, and their implications across various domains.

Understanding Wavenumber: Unlocking the Spatial Scale of Waves

In the intricate world of wave theory, the concept of wavenumber emerges as a fundamental cornerstone, often revered as the spatial counterpart to temporal frequency. Imagine it as a yardstick for measuring the spatial scale of waves, enabling us to grasp their intricacies and behavior in the vast expanse of space.

Exploring the Essence of Wavenumber:

• Spatial Frequency Unveiled: Wavenumber, also dubbed as the propagation number, delves into the spatial intricacies of waves, offering a nuanced understanding akin to how temporal frequency illuminates their temporal aspects;
• Spatial vs. Temporal: While temporal frequency focuses on the oscillations per unit time, wavenumber zeroes in on the oscillations per unit distance, giving rise to its moniker, the spatial frequency;
• Linguistic Labyrinth: Though often termed wavenumber in scientific parlance, it’s crucial to note that this concept is interchangeable with propagation number or spatial frequency, each shedding light on its unique facet;
• Wavelength Dance: At its core, wavenumber is intricately linked with the wavelength (λ), offering a measure of the number of wavelengths per unit distance, thereby encapsulating the essence of spatial dynamics within waves.

Deciphering the Math of Wavenumber:

At first glance, the mathematical underpinnings of wavenumber may appear daunting, akin to navigating a labyrinth of equations and derivations. However, beneath this veneer lies a surprisingly intuitive framework waiting to be unraveled.

• Definition Delve: Wavenumber, defined as the number of wavelengths per unit distance, unveils its essence through a simple yet profound equation, offering a gateway to deciphering its mathematical realm;
• Lambda Link: Expressed in terms of the wavelength (λ), wavenumber’s mathematical formulation intertwines intricately with its spatial counterpart, weaving a tapestry of spatial intricacies;
• Unit Unraveling: While the units of wavenumber are designated as m⁻¹ in the International System, their roots delve deeper into the centimetre-gram-second (cgs) system, where they don the moniker of “kaysers,” a testament to their rich historical lineage.

Navigating the Units of Wavenumber:

Embark on a journey through the labyrinth of units as we unveil the enigmatic realm of wavenumber measurements, shedding light on its significance and historical underpinnings.

• Unitary Unveiling: The units of wavenumber, succinctly denoted as m⁻¹, pave the path towards understanding the spatial intricacies of waves, encapsulating the essence of their propagation in a single numerical entity;
• Historical Echoes: Delve into the annals of scientific history, and you’ll stumble upon the centimetre-gram-second (cgs) system, where the units of wavenumber were christened as “kaysers,” echoing the scientific luminaries who pioneered their conceptualization;
• Interdisciplinary Insights: Beyond its numerical representation, wavenumber serves as a bridge between various scientific disciplines, intertwining physics, mathematics, and engineering in a symphony of spatial dynamics.

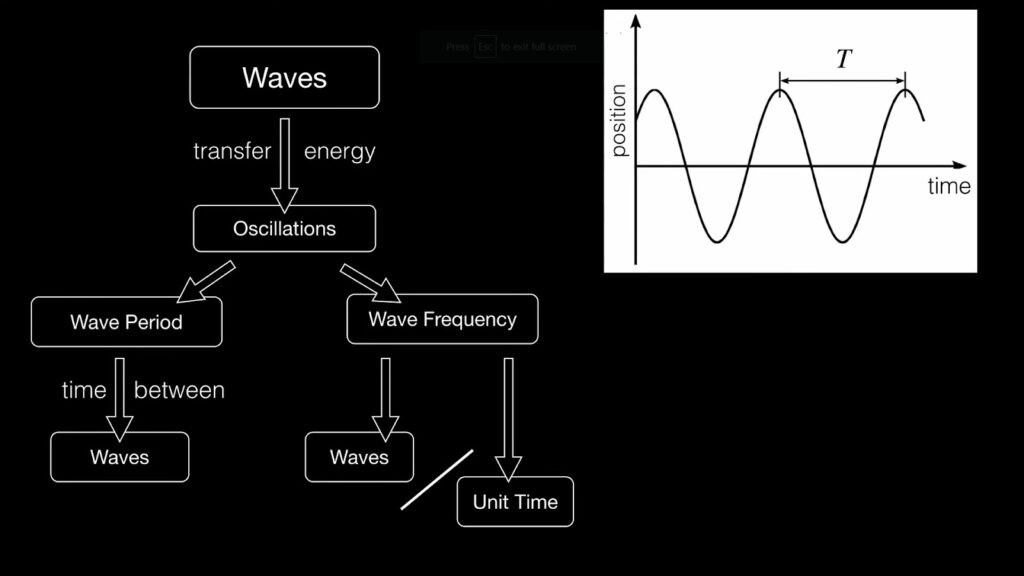
Analogy to Frequency and Period

The concept of wavenumber is analogous to frequency (f), which is measured in s–1 or Hertz. The frequency is essentially the reciprocal of the period (T), i.e., f = 1/T.

Drawing parallels between these concepts, we can consider the period as a temporal ‘wavelength.’ It signifies the length of an oscillation in time. This deep connection provides a broader perspective on the intricate interplay between space and time in wave theory.

• Frequency measures how often something happens over a particular duration;
• Period refers to how long each event or cycle lasts;
• Wavenumber measures how many wavelengths fit in a certain space.

Understanding these fundamental aspects of wave theory will grant a comprehensive insight into the dynamics of our environment, from the oscillations of ocean tides to the propagation of light and sound waves.

The Role of Angular Wavenumber in Geophysics

A deep dive into the realm of geophysics exposes us to an assortment of applications for frequency. Unlike the classical use of frequency, quantified in Hertz, geophysics often employs something called ‘angular frequency’. This alteration in methodology is a response to the intricacies of handling oscillating waveforms, which tend to fluctuate around a central value.

Visualize seismic data represented as a continuous line, oscillating or ‘wiggle’ trace. The waveform’s behavior in these applications underscores the need for a more nuanced approach: the angular frequency. The angular frequency not only encapsulates the frequency of these waveforms but also their phase, which is an angle. It’s a comprehensive concept that ties together frequency, phase, and the spatial dimension, making it highly valuable in geophysics.

The angular wavenumber, for instance, is expressed in radians per meter:

Note: Mathematical computation not provided.

Much like its relationship with frequency, the angular wavenumber’s connection to angular frequency parallel’s the correlation between wavelength and ordinary frequency. The velocity (V), ties these parameters together.

The Angular Wavenumber and Frequency

The relationship between the angular frequency and the angular wavenumber is a significant aspect of wave theory. This link has vital implications in geophysics, especially in the understanding of seismic waves, sound waves, light waves, and other electromagnetic radiation analyses.

This connection is encapsulated in the equation:

Note: Mathematical computation not provided.

For the uninitiated, here’s how to make sense of the above-mentioned concepts:

• Wavelength: The distance between similar points in the wave cycle, such as crest-to-crest or trough-to-trough;
• Frequency: The number of complete wave cycles passing a point in a second — measured in Hertz (Hz);
• Velocity: The rate at which the wave travels through a medium — measured in meters per second (m/s);
• Angular wavenumber: The spatial analog of angular frequency — expressed in radians per meter.

By exploring these principles, we can shed light on the underlying physics that govern the world around us, enabling us to predict and analyze geological activities more accurately.

Demystifying Wavenumber: Navigating Through The Confusion

Understanding wavenumber can be a bit perplexing due to the myriad of definitions employed by different individuals and sectors. Some prefer to deem it as spatial frequency, using Greek nu (ν) or sigma (σ) for labeling. However, a significant number of individuals adhere to the term ‘wavenumber’, symbolizing it with ‘k’. Such diversity in nomenclature often leads to confusion, necessitating clarity and precision in deploying these terms.

To traverse this linguistic labyrinth, one must always explicitly define the terms and their specific meanings within the given context. In doing so, the intentional clarity can help to bypass any potential misunderstanding.

The Fourier Transform: A Doorway To Understanding Wavenumber

Just like temporal frequency, the concept of wavenumber becomes more tangible through the Fourier Transform. This transformative mathematical tool computes along each spatial axis, providing a graphical demonstration that aids comprehension.

Consider two images and their respective 2D spectra – an image capturing ripples and another depicting binary particles. The fast Fourier transforms of these images serve as illustrative spectrums.

It’s fascinating to note that the spectrum of the more structured image exhibits a higher degree of organization. However, it may also show artifacts resulting from post-processing on the image. In contrast, the noisy image’s spectrum appears almost ‘white’, indicating a lack of organization and structure.

Features to observe in these spectrum images include:

• Organized spectrums tend to represent more structured images;
• Noisy or disorganized spectrums generally indicate randomness or lack of structure within the original image;
• Artifacts from post-processing on an image can influence the spectrum, introducing ‘false’ elements that don’t originate from the original image.

Understanding these elements brings us closer to a comprehensive understanding of wavenumber, helping us interpret and analyze a wide range of phenomena more effectively. From seismic investigations to photo analyses, the Fourier Transform serves as a versatile tool in connecting the dots between theory and practice. Read about the fascinating world of improbability in our article on unlikelihood. Discover rare occurrences and unexpected twists that defy expectations.

Conclusion

In conclusion, the concept of wavenumber plays a crucial role in understanding spatial characteristics within various fields. Serving as the spatial equivalent of temporal frequency, it provides a detailed measure of how wave patterns are distributed over a given distance. By quantifying the number of wavelengths within a unit distance, or through its relationship with wavelength λ, wavenumber offers a fundamental tool for analyzing wave phenomena in both theoretical and applied contexts. This measurement not only enhances our comprehension of spatial scales but also bridges the gap between spatial and temporal analyses, making it indispensable in the study of wave dynamics.